A 5-Point Minimal Solver for Event Camera Relative Motion Estimation
Oct 2, 2023·
,
,
,
,
,
·
1 min read
Ling Gao
Su Hao
Daniel Gehrig
Marco Cannici
Davide Scaramuzza
Laurent Kneip
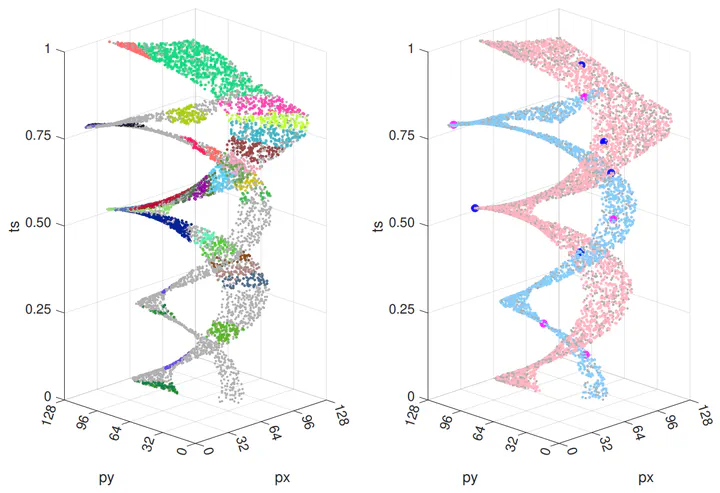
Abstract
Event-based cameras are ideal for line-based motion estimation, since they predominantly respond to edges in the scene. However, accurately determining the camera displacement based on events continues to be an open problem. This is because line feature extraction and dynamics estimation are tightly coupled when using event cameras, and no precise model is currently available for describing the complex structures generated by lines in the space-time volume of events. We solve this problem by deriving the correct non-linear parametrization of such manifolds, which we term eventails, and demonstrate its application to eventbased linear motion estimation, with known rotation from an Inertial Measurement Unit. Using this parametrization, we introduce a novel minimal 5-point solver that jointly estimates line parameters and linear camera velocity projections, which can be fused into a single, averaged linear velocity when considering multiple lines. We demonstrate on both synthetic and real data that our solver generates more stable relative motion estimates than other methods while capturing more inliers than clustering based on spatiotemporal planes. In particular, our method consistently achieves a 100% success rate in estimating linear velocity where existing closed-form solvers only achieve between 23% and 70%. The proposed eventails contribute to a better understanding of spatio-temporal event-generated geometries and we thus believe it will become a core building block of future event-based motion estimation algorithms.
Type
Publication
Int. Conf. Comput. Vis. (ICCV)
This paper lead to an oral at ICCV 2023 in Paris!